介紹穩定子編碼的基本概念、Pauli 運算、量子糾錯原理,以及 Shor’s、Steane 和 Surface codes 的實務應用。涵蓋 Google 2023 年的實驗驗證成果。
前言
量子計算的發展面臨一個根本性挑戰:量子錯誤。與經典計算不同,量子系統極其脆弱,環境中的任何干擾 (溫度波動、電磁噪音、晶片的製造缺陷) 都會導致 qubits 產生錯誤。更棘手的是,我們無法簡單地複製量子態來進行備份,這個限制被稱為「無複製定理」 (no-cloning theorem)。
然而,理論物理學家們發現了一條出路:量子糾錯碼 (quantum error correcting codes)。這些碼的核心思想是將邏輯信息巧妙地編碼到多個物理 qubits 中,使得即使部分 qubits 發生錯誤,邏輯信息仍可被恢復。這聽起來似乎是一個悖論:更多的 qubits 意味著更多可能出錯的地方,但在「容錯閾值」之下,這種編碼方式確實有效。
穩定子編碼 (stabilizer codes) 是量子糾錯領域中最成功的框架。它使用一組特殊的可觀測量 (稱為「穩定子」) 來非破壞性地偵測錯誤,而不會摧毀被保護的量子信息。從 1995 年 Peter Shor 提出的第一個量子糾錯碼,到 2003 年 Alexei Kitaev 發現的拓撲量子碼,再到今天 Google 等企業正在實現的 Surface codes,穩定子編碼已經演化成一套完整、優雅的理論體系。
本文將帶你深入理解穩定子編碼的核心概念。我們從 Pauli 矩陣和其基本性質出發,逐步構建起量子糾錯的基礎。然後介紹三個經典的實現方案 (Shor code、Steane code 和 Surface code) 展示不同的設計思想和工程權衡。最後,我們會看到 Google 2023 年的實驗成果,它首次驗證了「更大的碼在實驗上確實表現更好」這一基本假設,為未來的容錯量子計算指引了方向。
無論你是量子計算的初學者還是專業研究者,這篇文章的目的是幫助你建立一個系統化的理解:從理論基礎、到實務設計、再到現實驗證。
Pauli 運算 (Pauli Operations)
為何要介紹 Pauli 運算:
Pauli 算符是構成單位量子運算的基礎元件。了解 I, X, Y, Z 的代數性質(交換關係與乘法規則)對後續的 stabilizer formalism、錯誤類型識別、syndrome 推導與解碼器設計至關重要。具體原因包括:
- 表示能力:透過張量積,n‑qubit 的任意 Pauli 運算都可以由單比特 Pauli 算符組成,作為分析錯誤的自然基底。
- 錯誤對應:位錯 (bit‑flip) 與相錯 (phase‑flip) 分別對應
X和Z,而Y可表示為i X Z,因此在 Pauli 基底下分析能直接對應到要偵測與更正的錯誤類型。 - 穩定子核心:stabilizer code 的生成元即為 Pauli 類算符,其交換/反換易性質決定錯誤是否會改變 stabilizer 的量測結果。
- 實驗與模擬便利:X/Z 的量測與受控‑Pauli 操作是實務上常用的工具,許多誤差模型與模擬技術 (例如 Pauli twirling) 也在此基底下更易處理。
Pauli 矩陣與單位矩陣為:
$$
I=\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix},\quad
X=\begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix},\quad
Y=\begin{pmatrix}0 & -i \\ i & 0\end{pmatrix},\quad
Z=\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}
$$
反換易 (anti-commutation) 關係:
- $XY = -YX$
- $XZ = -ZX$
- $YZ = -ZY$
乘法規則:
- $XY = iZ$
- $YZ = iX$
- $ZX = iY$
- $XX = YY = ZZ = I$
所謂的 n-qubit Pauli 運算,就是把每個 qubit 的 Pauli 矩陣做張量 (tensor) 相乘得到的 n 重張量積。這個運算的「weight」指的是張量積中非單位矩陣 (非 $I$) 的個數。
範例:
I ⊗ I ⊗ I ⊗ I ⊗ I ⊗ I ⊗ I ⊗ I ← weight 0
X ⊗ X ⊗ I ⊗ I ⊗ I ⊗ I ⊗ I ⊗ I ← weight 2
X ⊗ X ⊗ Y ⊗ Z ⊗ I ⊗ I ⊗ X ⊗ Y ← weight 6
以上關係與範例在討論 stabilizer code (穩定子編碼) 或多 qubit Pauli 運算性質時非常常用,後面如果講 stabilizer formalism 可以直接引用這裡的定義。
Pauli 可觀測量 (Pauli Observables)
Pauli 矩陣除了描述單位演化外,也能對應到投影型量測 (projective measurement) ,由它們的本徵向量定義對應的投影算符。
以算符形式表示:
- $X = |+\rangle\langle+| - | - \rangle\langle - |$
- $Y = |+i\rangle\langle+i| - |-i\rangle\langle -i|$
- $Z = |0\rangle\langle0| - |1\rangle\langle1|$
這裡每個 Pauli 可觀測量的本徵值是 $+1$ 或 $-1$,對應的投影算符 (projectors) 可以寫成 $\{ |\psi_+\rangle\langle\psi_+|,; |\psi_-\rangle\langle\psi_-| \}$,其中 $|\psi_\pm\rangle$ 是該可觀測量對應的本徵態。
舉例來說,對 $X$ 的量測就是以基底 ${ |+\rangle, | - \rangle}$ 進行,等價地可以用投影集合 $\{ |+\rangle\langle+|,; | - \rangle\langle- | \}$ 描述。量測結果會是本徵值 $+1$ 或 $-1$ (常標記成 0/1 或 +/−),對應的本徵態是被投影出來的結果。
概念上如下圖,可以用相位估測 (phase estimation) 的一種方式,非破壞性 (non-destructively) 地讀出這些 Pauli 可觀測量的本徵值:把被測系統作為受控作用 (controlled‑U) 的 target,再將本徵值資訊寫到輔助量子位元上,讀出輔助位元即可得知本徵值 (+1 或 −1),而被測系統態在理想情況下仍保留在對應的本徵態上。相關技術詳見 Understanding Quantum Information & Computation。
Non-destructively measure; source
總結要點:
- Pauli 矩陣同時定義了對應的 projective measurement;量測基底就是其本徵態。
- 量測結果對應本徵值 +1 / −1,或等價的「測量符號」。
- 若需要非破壞性地知道本徵值,可以用相位估測等技術把本徵值寫到輔助位元再讀出。
偵測錯誤 (Detecting errors)
設 $P_1,\dots,P_r$ 為一個 n‑qubit stabilizer code 的 stabilizer generators,令 $E$ 為一個 n‑qubit Pauli 運算 (代表一個假設的錯誤) 。透過量測 stabilizer generators (把每個 generator 當成一個 Observable 量測) ,可以偵測錯誤;r 個量測結果合起來就形成了 syndrome。
以下列出常見的三種情況:
- 若存在 $Q\in\langle P_1,\dots,P_r\rangle$ 使得 $E=\alpha Q$:錯誤對 code space 的向量沒有實質影響。對任一被編碼態 $|\psi\rangle$,都有 $E|\psi\rangle = \alpha|\psi\rangle$ (僅產生整體相位) ,因此 stabilizer 量測不會偵測到差異。
- 若 $E \neq \alpha Q$ 對任一 $Q\in\langle P_1,\dots,P_r\rangle$,但 $E$ 與每一個 generator 都交換:錯誤會改變 code space 中的態,但因為它與所有 stabilizer 交換,stabilizer 量測結果不會改變,意即錯誤沒有被 code 偵測到 (undetected)。
- 若存在至少一個 $k$ 使得 $P_k E = - E P_k$:錯誤會改變 stabilizer 的測量結果,因此可以被 code 偵測到 (detected)。
根據上面情形,我們定義 stabilizer code 的 distance:code 的距離 (distance) 是改變 code space 向量但被 code 未偵測到 (undetected) 的 Pauli 運算中,最小的 weight (weight 在前面已有定義,指的是張量積中非 $I$ 的個數) 。簡單來說:distance = 最小的可導致不可偵測錯誤的 Pauli weight。
常見記號:一個 [[n, m, d]] 的 stabilizer code 表示它把 $m$ 個 logical qubits 編碼到 $n$ 個 physical qubits,且具有距離 $d$。
備註 (直觀理解) :distance d 表示 code 至少能夠容忍 (d-1)/2 的位錯 (bit-flip) 或相錯 (phase-flip) (具體可容錯數目需視錯誤類型與糾錯演算法) ,distance 越大代表能耐受或訂正的錯誤越多,但同時需要更多的實體 qubits。
為什麼量測不會影響 data qubits?
用於 stabilizer 量測的常見設計能夠把「量測資訊」安全地寫到輔助位元 (measure qubits / ancilla) 上,而不直接讀出或破壞 data qubits 的邏輯信息。關鍵要點:
- 用 ancilla 擷取 parity:一個典型步驟是先把 data qubits 的 parity (或穩定子算符的本徵值) 透過一系列受控‑Pauli 閘 (例如 CNOT) 映射到一個 ancilla qubit 上,接著量測 ancilla。量測結果給出 stabilizer 的 ±1,本體的 data qubits 僅被投影到對應的 stabilizer 本徵子空間中,而不會直接暴露邏輯位元的相位或振幅。
- 穩定子與邏輯運算的關係:stabilizer 生成元被刻意設計成與邏輯算符 (logical operators) 互換 (commute),因此測得的 stabilizer 本徵值不會提供關於邏輯量子態的資訊;也就是說,量測 stabilizer 只會顯示錯誤的存在與位置,而不會將邏輯超位置崩潰。
- 非破壞性與重複量測:量測 ancilla 並重新初始化後,可以重複執行 syndrome 提取以減少瞬時讀取錯誤的影響。這種「擷取‑讀出‑重置」模式使得我們能頻繁取得 syndrome 而不破壞儲存在 data qubits 上的邏輯信息。
- 容錯實作注意事項:為避免 ancilla 錯誤回傳到多個 data qubits(error propagation),實務上會使用經驗證的 ancilla 狀態、分段映射、或額外的驗證閘(例如使用 cat state 並驗證其正確性)以保持 syndrome 提取的容錯性。這些技術確保量測流程自身不會成為主要的錯誤來源。
為什麼只需要量測 X 和 Z 錯誤?
在穩定子編碼的錯誤偵測中,一個常見的問題是:為什麼我們只量測 X-type 和 Z-type 穩定子,而不直接量測 Y 錯誤?
答案在於 Pauli 群的代數結構。根據 Pauli 矩陣的乘法關係:
$$Y = iXZ$$
這表示一個 Y 錯誤等價於同時發生 X 錯誤和 Z 錯誤 (忽略全域相位 $i$,因為全域相位不影響量測結果)。
當我們設計穩定子編碼時:
- X-type stabilizers 能偵測到 Z 錯誤 (及包含 Z 的錯誤如 Y)
- Z-type stabilizers 能偵測到 X 錯誤 (及包含 X 的錯誤如 Y)
如果一個 Y 錯誤發生在某個 qubit 上,它會同時違反該位置相關的 X-type 和 Z-type 穩定子。透過這兩類穩定子的量測結果組合 (syndrome pattern),我們能唯一識別出 Y 錯誤的位置。
從數學角度來看,選擇 X 和 Z 作為生成元 (generators) 已經可以張成整個 n-qubit Pauli 群,Y 不提供額外的獨立信息。從實驗角度來看,只量測 X 和 Z 有實務優勢:
- X 量測對應 $|+\rangle, |-\rangle$ 基底,Z 量測對應 $|0\rangle, |1\rangle$ 基底,都是標準量測基底
- Y 量測需要額外的基底旋轉 (如 $S^\dagger$ 或 Hadamard + phase gate),增加電路複雜度
- 減少量測次數降低了操作開銷和錯誤累積
因此,量測 X 和 Z 穩定子已經足夠完整地診斷包括 Y 在內的所有單 qubit Pauli 錯誤。
真實案例:經典的穩定子編碼
下面介紹三個經典且重要的 stabilizer codes,幫助理解如何從理論設計出實用的量子糾錯方案。
Shor’s Code [[9, 1, 3]]
歷史背景:Shor’s code 是 1995 年 Peter Shor 提出的第一個量子糾錯碼,具有里程碑意義。它展示了量子錯誤糾正是可行的,激發了後續的大量研究。
編碼方式:Shor’s code 把 1 個 logical qubit 編碼到 9 個 physical qubits,採用「重複 + 糾纏」的混合策略:
- 先用 3 個 qubits 的重複碼來對抗相位反轉錯誤 (phase-flip)。
- 再把每一位用 3 個 qubits 做 GHZ 態般的糾纏,用來對抗位反轉錯誤 (bit-flip)。
參數:[[9, 1, 3]] 表示 9 個 physical qubits、1 個 logical qubit、距離 3。
Stabilizer 生成元 (8 個) :
- 相位錯誤偵測:$Z_1 Z_2$, $Z_2 Z_3$, $Z_4 Z_5$, $Z_5 Z_6$, $Z_7 Z_8$, $Z_8 Z_9$
- 位錯誤偵測:$X_1 X_2 X_3$, $X_4 X_5 X_6$, $X_7 X_8 X_9$
(注:上面只列舉一部份;完整的 Shor code 還有更多生成元的交配關係。)
特點與限制:
- 實現相對直接,易於理解。
- 能糾正單個位錯誤或單個相位錯誤。
- 9 個物理位對 1 個邏輯位的開銷相當大 (overhead 很高) 。
- 實務上已被更高效的碼 (如 Steane code 或 Surface code) 取代。
Steane’s Code [[7, 1, 3]]
特色:Steane code 把 1 個 logical qubit 編碼到 7 個 physical qubits,比 Shor’s code 更精緻高效,是第一個達到「css code」範疇的例子。
CSS Code 的概念:CSS (Calderbank-Shor-Steane) 碼是一類特殊的穩定子碼,它把位糾錯和相位糾錯分開獨立設計,再結合起來。Steane code 正是 CSS 構造的典型例子。
參數:[[7, 1, 3]],比 Shor’s code 節省了 2 個 physical qubits。
Stabilizer 生成元 (6 個) :
- $X_1 X_2 X_3 X_4$
- $X_2 X_3 X_5 X_6$
- $X_3 X_4 X_6 X_7$
- $Z_1 Z_2 Z_3 Z_4$
- $Z_2 Z_3 Z_5 Z_6$
- $Z_3 Z_4 Z_6 Z_7$
(這些生成元來自 Hamming code 的奇偶校驗矩陣,體現了經典編碼與量子編碼的對應。)
特點與應用:
- 編碼密度相比 Shor’s code 提升,仍保有距離 3 的容錯能力。
- 展示了如何用經典編碼論的思想設計量子碼。
- 在理論研究與教學中仍被廣泛使用。
Surface Code (表面碼) 與 Toric Code (環面碼)
Toric Code 是由 Kitaev 在 2003 年提出的二維拓撲量子碼,具有革命性意義。它不僅展示了穩定子形式的威力,還引入了「拓撲序」(topological order) 的概念。
Surface Code 是 Toric code 在邊界上的變體,更適合在二維陣列上實作,是目前 NISQ (近期量子設備) 時代最被看好的容錯方案。其實現原理源於一個簡單的古典概念:在棋盤上放置 Data qubits 和 Measure qubits,透過非破壞性的穩定子量測來檢測錯誤位置。
在表面碼的二維陣列實作中,資料量子位以空心圓 (∘) 表示,測量量子位以實心圓 (•) 表示,其中 Z 測量量子位為深綠色,X 測量量子位為淺橘色。遠離邊界時,每個資料量子位會接觸四個測量量子位,而每個測量量子位也會接觸四個資料量子位,並進行四端測量。在邊界上,測量量子位只接觸三個資料量子位並進行三端測量,而資料量子位會接觸二或三個測量量子位。包圍陣列的實線表示陣列邊界。 source
特色與優勢:
- 二維格點結構:Stabilizer 只涉及相鄰 qubits 的交互作用,利於硬體實現 (不需要長程交互) 。
- 局部性:每個 stabilizer 生成元只牽涉 4 個相鄰 qubits (環) 或 2 個相鄰 qubits (邊) ,使得量測和控制都能在局部進行。
- 拓撲保護:錯誤必須在格點上形成「環路」(loop) 才能造成邏輯錯誤,單個孤立的錯誤容易偵測與糾正。
- 可擴展性:距離 $d$ 的 Surface code 需要約 $2d^2$ 個物理 qubits,邏輯位數可隨著格點大小擴展。
- 容錯閾值低:Surface code 的容錯閾值相對較低 (約 1%) ,在最近才變得實驗上可行。這意味著只要物理 qubits 的錯誤率低於此閾值,增加碼的大小就能指數級地改善邏輯 qubit 的表現。
Surface Code 結構示意:Data qubits (黃色) 位於棋盤的頂點構成邏輯 qubit,Measure qubits (藍色) 位於每個方形的中心。深藍色方塊檢測位反轉錯誤,淺藍色檢測相位反轉錯誤。當某個 stabilizer 量測偵測到錯誤時,相鄰的量測結果相關性被用來定位錯誤。 source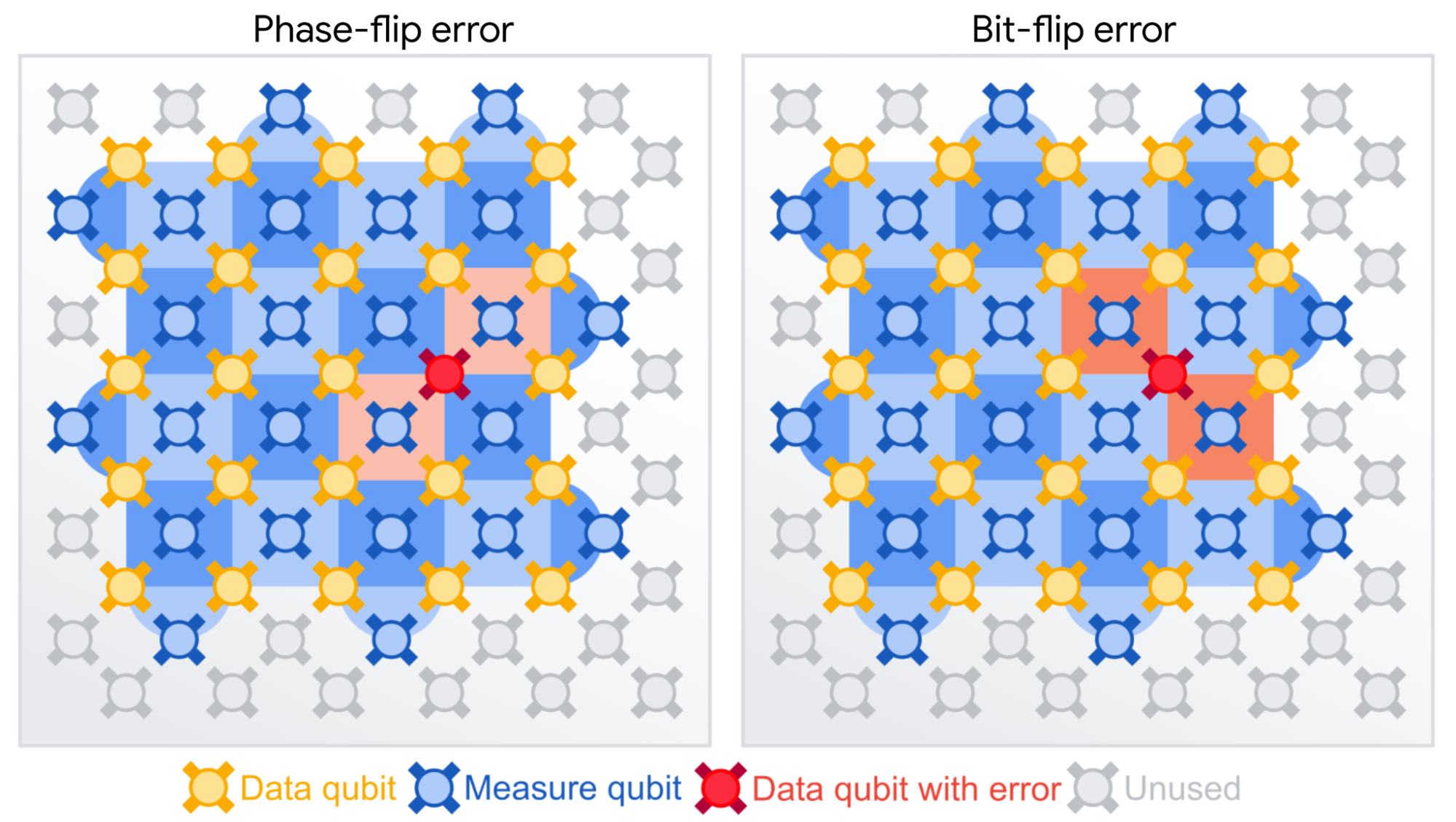
參數範例:一個 distance $d$ 的 Surface code 編碼 1 個 logical qubit,參數形式為 [[2d^2 - 2d, 1, d]] 或約為 [[~2d^2, 1, d]] (取決於邊界條件) 。
Stabilizer 生成元 (概念層級) :
- Plaquette operators (或稱 $B_p$):每個內部四邊形晶胞的四個 qubits 做 $Z Z Z Z$ 或 $X X X X$。
- Vertex operators (或稱 $A_v$):每個格點處的四個相鄰 qubits 做交叉作用。
(具體形式因邊界條件與規約而異;細節超出本文範圍。)
實務應用與前景:
- Google、IBM、Microsoft 等企業的近期容錯量子裝置研究都大量採用 Surface code 或其變體。
- 被認為是實現大規模量子計算的最有希望的路線。
- 與拓撲量子計算 (topological quantum computing) 的概念相關,可能帶來物理直觀的容錯機制。
Google 的 Surface Code 實驗驗證 (2023)
2023 年 2 月,Google Quantum AI 團隊在《Nature》期刊發表「Suppressing Quantum Errors by Scaling a Surface Code Logical Qubit」,報告了一個重要里程碑。這項工作經過三年的聚焦研究,旨在實現容錯量子計算。
實驗關鍵指標:
- 使用改進版的第三代 Sycamore 處理器,建構了兩個不同規模的 Surface codes:
- Distance 3:17 個 physical qubits
- Distance 5:49 個 physical qubits
- 實驗目標:比較兩個碼的邏輯錯誤率,用比值 Λ₃,₅ = ε₃ / ε₅ 衡量 (Λ > 1 表示距離大的碼效能更好)
- 核心問題:能否證明在足夠好的 physical qubits 下,增加碼的大小會改善邏輯 qubit 的表現?這是量子糾錯研究中最重要的實驗驗證。
實驗成果:
- Distance 5 碼的邏輯錯誤率 (ε₅ = 2.914%) 優於 Distance 3 碼 (ε₃ = 3.028%)
- 改進幅度:Λ₃,₅ = 1.04 (5σ 信心水準,約 4% 的改進)
- 這是歷史上第一次 (自 Peter Shor 1995 年提案以來) 驗證了「更大的碼在實驗上確實表現更好」這一關鍵假設
邏輯保真度對比:左圖顯示距離 3 與距離 5 的 Surface code 配置。右圖為改進過程中的數據點,顯示隨著時間推進,distance-5 碼的保真度最終超越 distance-3 碼,兩條線在右上方的交點表明更大的碼表現更好。 source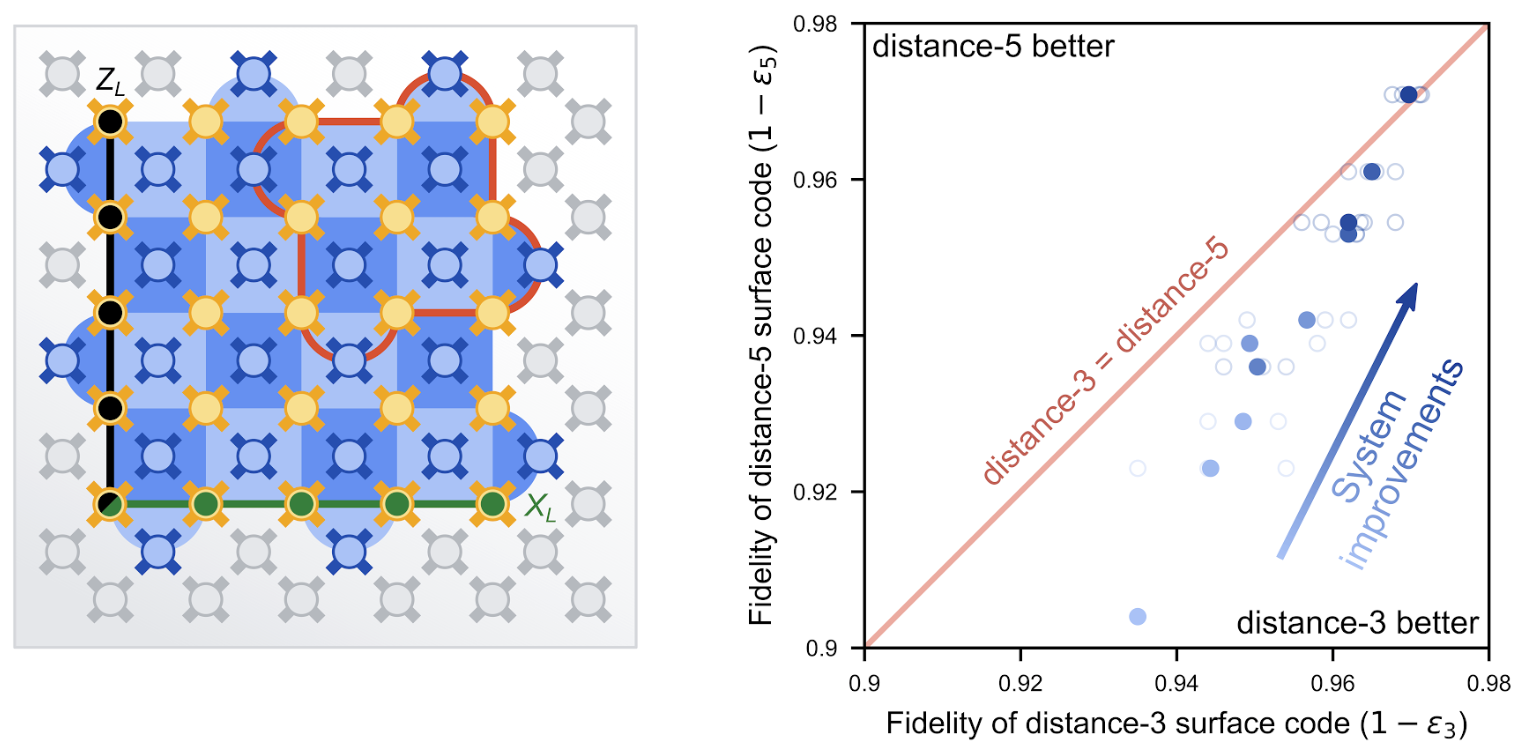
技術突破:為了達成這個成果,Google 團隊進行了全面的硬體改進:
- 改善 qubit 鬆弛和去相干時間,透過改進的製造工藝和減少量子處理器附近的環境雜訊
- 降低 qubit 間的串擾 (cross-talk),通過優化量子處理器電路設計和奈米製造工藝
- 提升 readout 和 reset 操作的保真度,相比前幾代 Sycamore 處理器有顯著改進
- 增強動力學解耦 (dynamical decoupling) 協議,保護物理 qubits 在空閒時免受雜訊和串擾
- 最佳化全系統校準算法,通過廣泛建模完整量子系統並採用更好的系統優化演算法減少校準誤差
- 實現上下文感知和完全平行校準,最小化漂移並優化量子糾錯電路的控制參數
- 升級自訂電子設備以降低漂移並改進 qubit 控制保真度
邁向容錯的路線圖:
Google 容錯量子計算路線圖與誤差目標:左圖顯示預期的進展方向,其中 Λ (距離 3 與距離 5 碼的錯誤率比值) 與碼距離之間的關係。右圖為實驗測得的邏輯誤率隨碼距離變化的曲線,顯示 distance-25 的重複碼已接近 1/10⁶ 的目標。 source
- 目標:達成邏輯錯誤率 ≤ 1/10⁶ per cycle (工業應用所需)
- 預估需要距離 17 的 Surface code,約 577 個高品質 physical qubits
- 預期未來數年達成此目標後,進入「容錯機制」(fault-tolerant regime),屆時邏輯錯誤會隨碼規模指數級下降
- 實驗技術表明,通過一維重複碼 (repetition codes) ,已可達到約 1/10⁻⁶ 的低錯誤率
相關進度與詳細結果,請參閱 Google 研究部落格。
實驗成果的深遠意義
這個結果看似微小 (只有 4% 的改進) ,但其重要性不容小覷。它代表了量子糾錯研究中的一個關鍵里程碑:
- 歷史意義:這是自 Peter Shor 在 1995 年提出量子糾錯概念以來,第一次在實驗上驗證「更大的碼在實驗上確實表現更好」這一基本假設。在此之前,儘管理論上應該如此,但由於 physical qubits 的高錯誤率,實驗中往往觀察不到這個現象。
- 技術突破:Google 的工作表明,通過足夠精心的硬體優化和系統設計,可以使物理 qubits 的錯誤率降低到足以實現容錯量子計算的水平。這需要在多個層面同時進行改進:從晶片設計、製造工藝、控制電子、到量子演算法的優化。
- 路徑指示:實驗結果給出了明確的發展方向。通過繼續改進物理 qubits 的質量 (使 Λ 值從接近 1 增加到更大的值) ,並擴大碼的規模 (增加 distance) ,可以預期在未來數年內達到 1/10⁶ 的錯誤率目標,從而進入「容錯機制」(fault-tolerant regime)。
- 物理意義:這個成果代表量子糾錯已從「能否可行」的理論問題,轉向「如何大規模擴展」的工程挑戰。它證明了在足夠精心的硬體優化下,Surface code 能夠跨越「fault-tolerant threshold」,為未來的實用量子計算奠定基礎。
對比總結:
| 碼 | 參數 | 物理位/邏輯位 | 局部性 | 硬體難度 | 應用前景 |
|---|---|---|---|---|---|
| Shor | [[9, 1, 3]] | 9 | 無 (長程交互) | 低 | 教學、理論驗證 |
| Steane | [[7, 1, 3]] | 7 | 無 (長程交互) | 低 | 教學、理論研究 |
| Surface | [[~2d², 1, d]] | ~2d² | 是 (只需近鄰交互) | 高但可擴展 | 產業應用、實驗驗證 |
參考資料
- The Stabilizer Formalism | Understanding Quantum Information & Computation | Lesson 14
- Peter W. Shor. “Scheme for reducing decoherence in quantum computer memory,” Phys. Rev. A , vol. 52 , pp. R2493-R2496. 1995. DOI: 10.1103/PhysRevA.52.R2493.
- A. M. Steane. “Error Correcting Codes in Quantum Theory,” Phys. Rev. Lett. , vol. 77 , pp. 793-797. 1996. DOI: 10.1103/PhysRevLett.77.793.
- A.Yu. Kitaev. “Fault-tolerant quantum computation by anyons,” Annals of Physics , vol. 303 , no. 1, pp. 2-30. 2003. DOI: 10.1016/S0003-4916(02)00018-0. (Toric code 的原始論文)
- Austin G. Fowler, Matteo Mariantoni, John M. Martinis, and Andrew N. Cleland. “Surface codes: Towards practical large-scale quantum computation,” Phys. Rev. A , vol. 86 , pp. 032324. 2012. DOI: 10.1103/PhysRevA.86.032324.
- Barbara M. Terhal. “Quantum error correction for quantum memories,” Rev. Mod. Phys. , vol. 87 , pp. 307-346. 2015. DOI: 10.1103/RevModPhys.87.307. (Surface code 綜合綜述)
本文部分內容由Claude Haiku 4.5 和 GPT-5 mini協助生成,作者具備相關專業能力,對 AI 產出內容進行審核與把關,並對文章的正確性負最終責任。若文中有錯誤之處,敬請不吝指正,作者將虛心接受指教並儘速修正。
